Dividing and Conquering a BlackBox to a Mixture of Interpretable Models: Route, Interpret, Repeat

Problem Statement. We aim to solve the problem of explaining the prediction of a deep neural network post-hoc using high level human interpretable concepts. In this work, we blur the distinction of post-hoc explanations and designing interpretable models.

Why post-hoc, not interpretable by design? Most of the early interpretable by design methods focus on tabular data. Plus, they tend to be less flexible than the Blackbox models and demand substantial expertise to design. Also, mostly they underperform than their Blackbox counterparts. Post hoc methods preserve the flexibility and performance of the Blackbox.

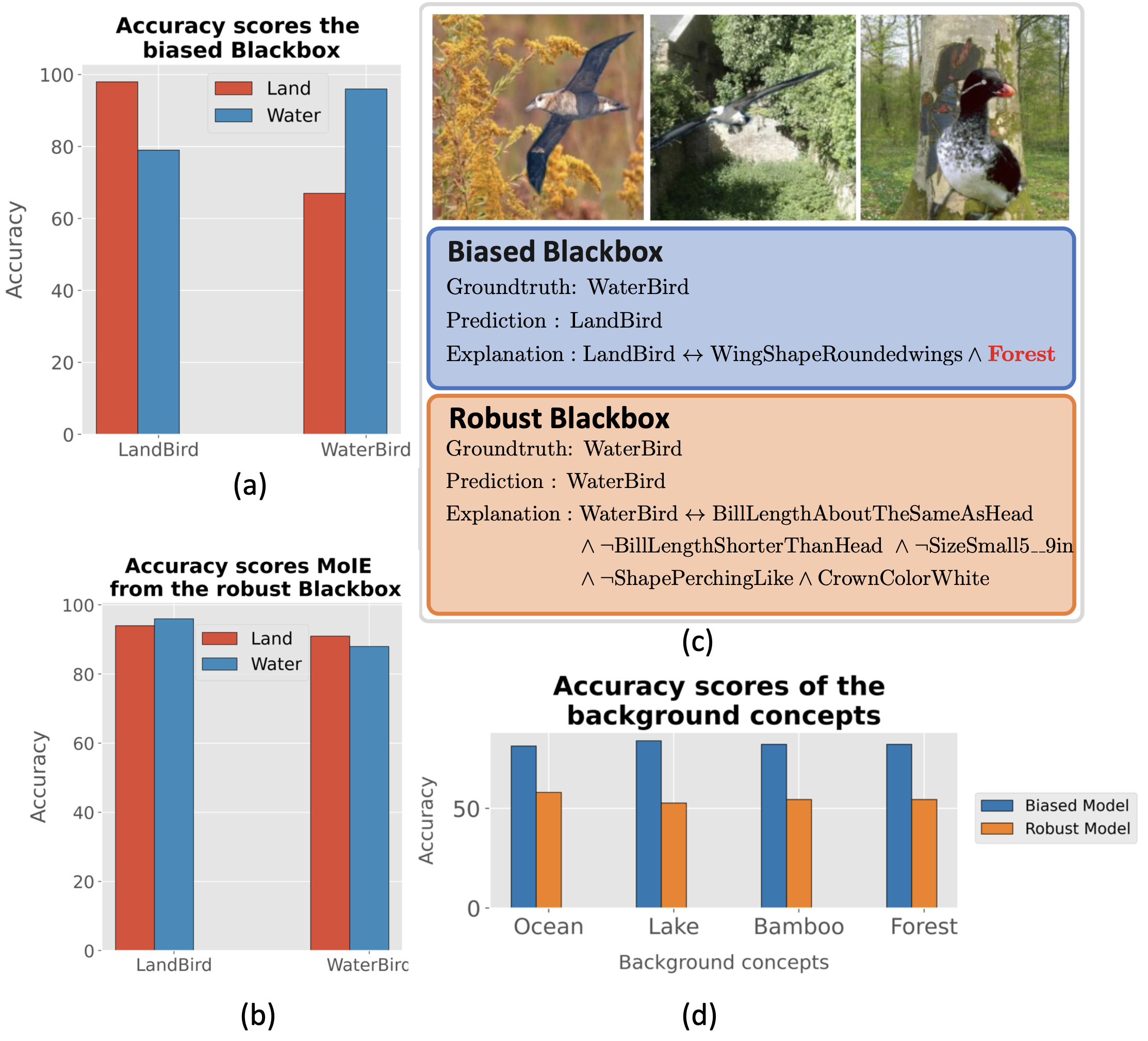
Why concept based model, not saliency maps? Post-hoc based saliency maps identify key input features that contribute the most to the network’s output. They suffer from a lack of fidelity and mechanistic explanation of the network output. Without a mechanistic explanation, recourse to a model’s undesirable behavior is unclear. 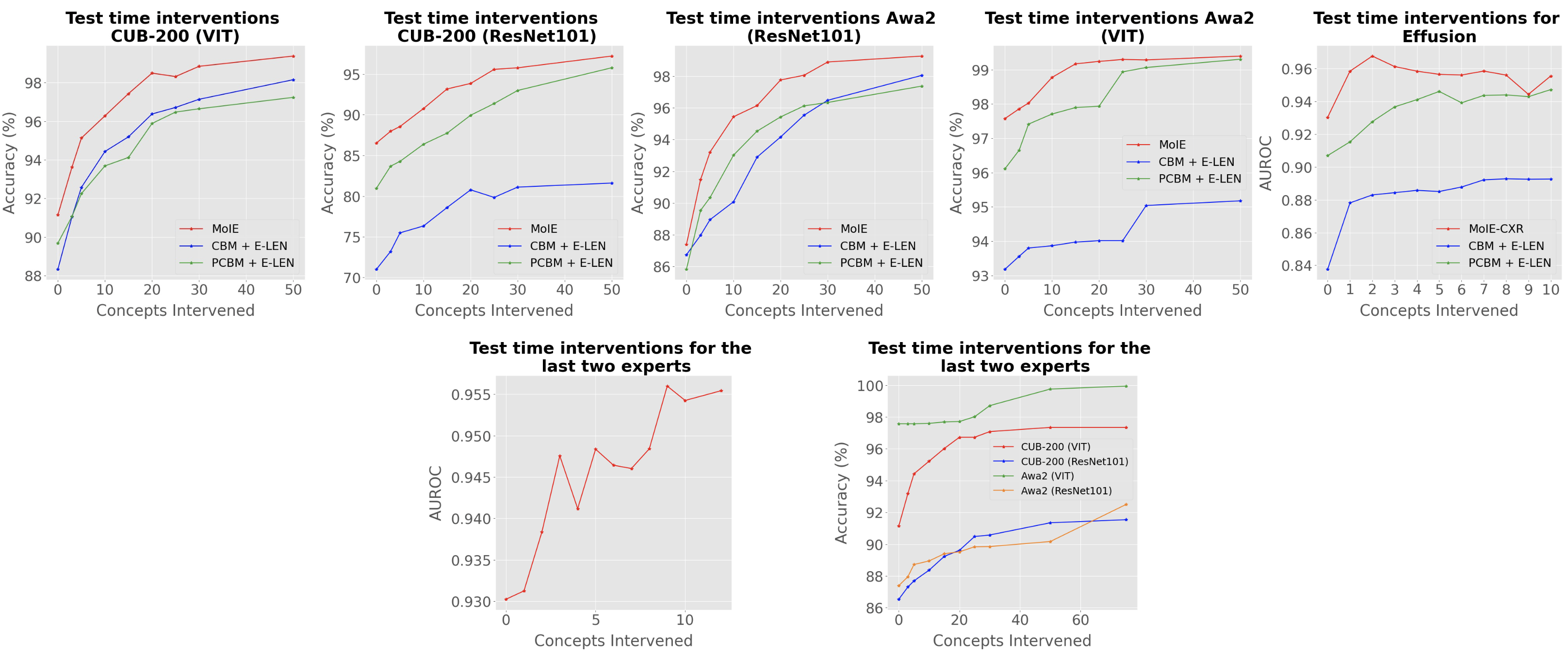Concept based models can identify the important concept, responsible for the model's output. We can intervene on these concepts to rectify the model's prediction.

What is a concept based model? Concept based model or technically Concept Bottleneck Models are a family of models where first the human understandable concepts are predicted from the given input (images) and then the class labels are predicted from the concepts. In this work, we assume to have the ground truth concepts either in the dataset (CUB200 or Awa2) or discovered from another dataset (HAM10000, SIIM-ISIC or MIMIC-CXR). Also, we predict the concepts from the pre-trained embedding of the Blackbox as shown in Posthoc Concept Bottleneck Models.

What is a human understandable concept? Human understandable concepts are high-level features which constitute the class label. For example, the stripes can be a human understandable concept, responsible for predicting zebra. In chest-x-rays, anatomical features like lower left lobe of lung can be another human understandable concept. For more details, refer to TCAV paper or Concept Bottleneck Models.

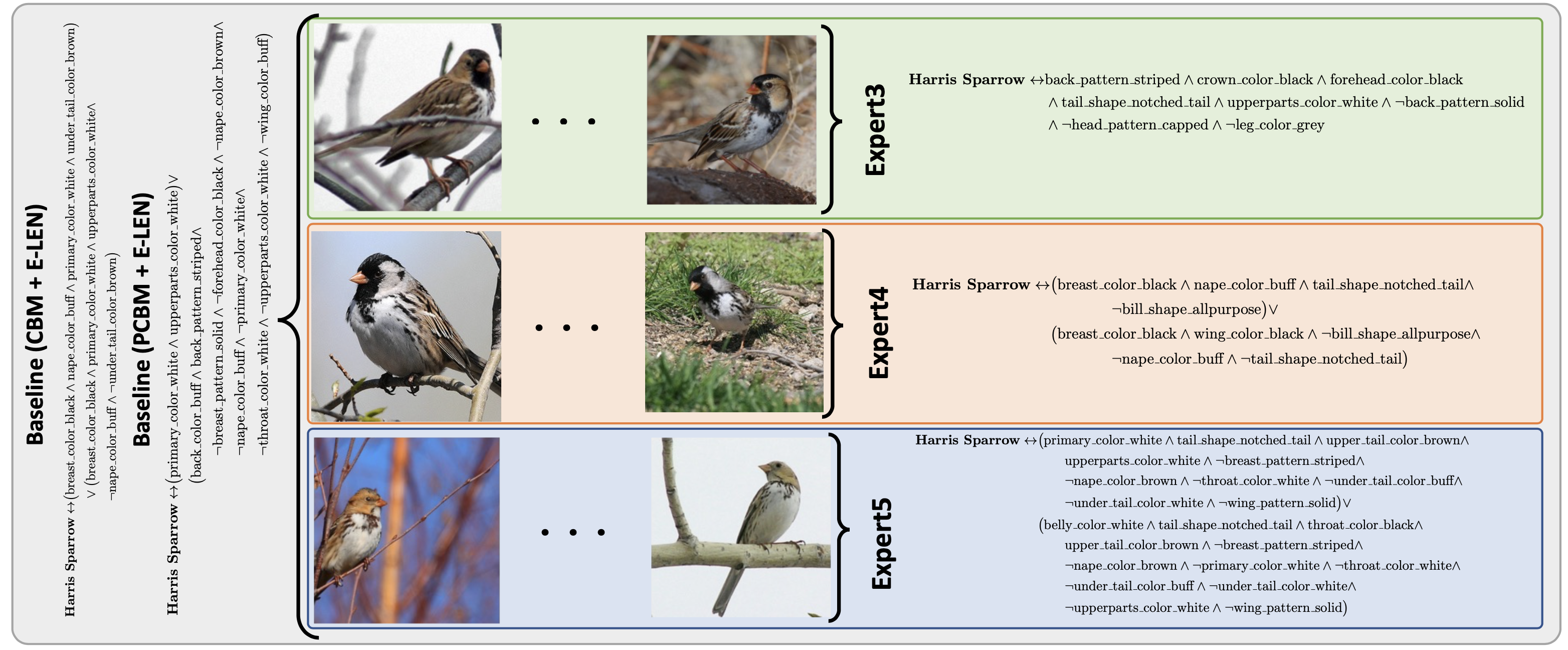
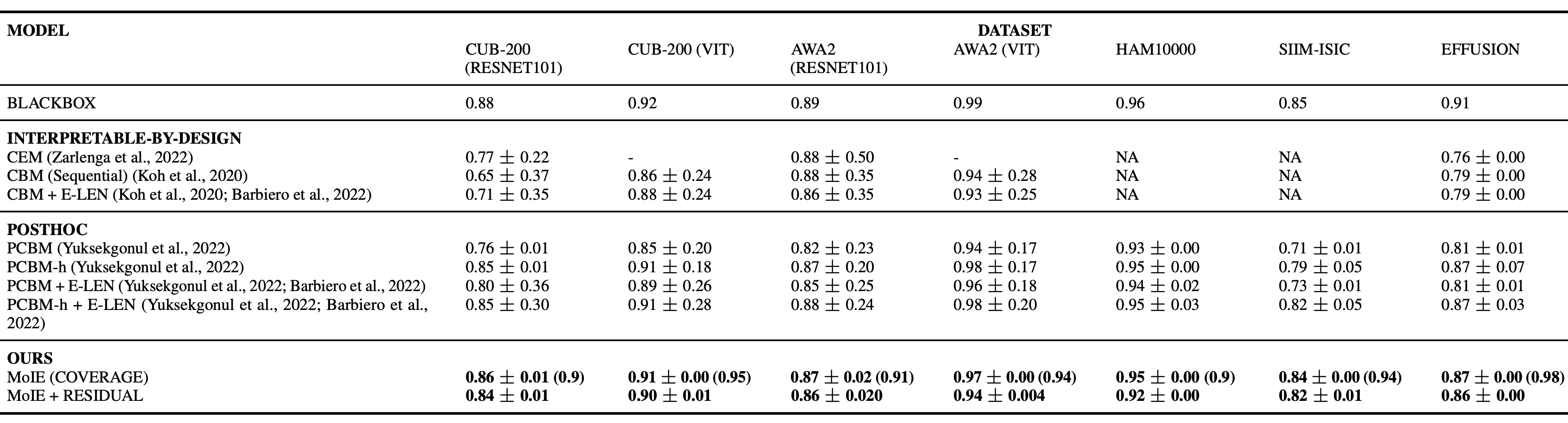
What is the research gap? Most of the interpretable models (interpretable by design or post-hoc) utilizes a single interpretable model to fit the whole data. If a portion of the data does not fit the template design of the interpretable model, they do not offer any flexibility, compromising performance. Thus, a single interpretable model may be insufficient to explain all samples, offering generic explanations.

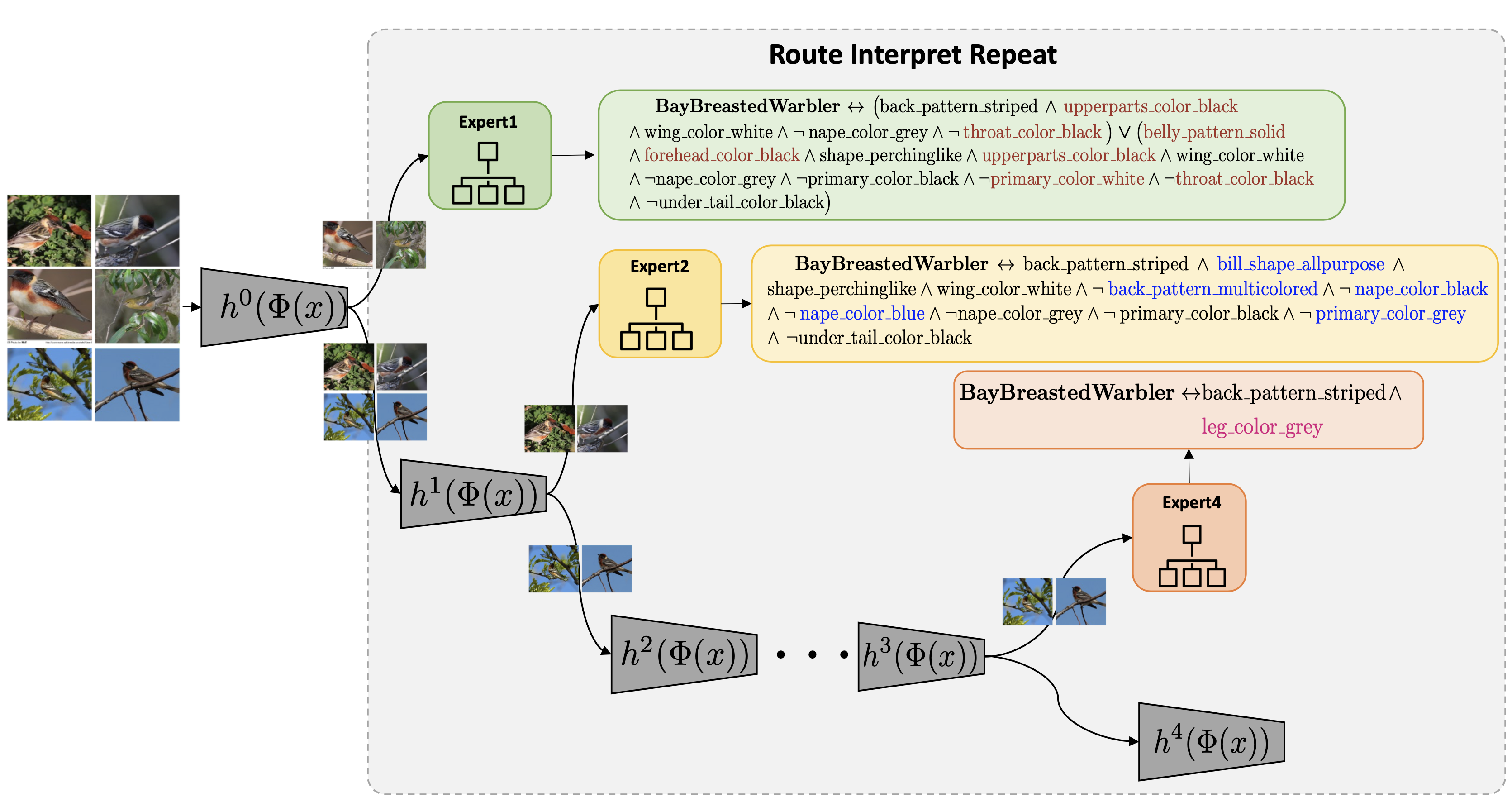
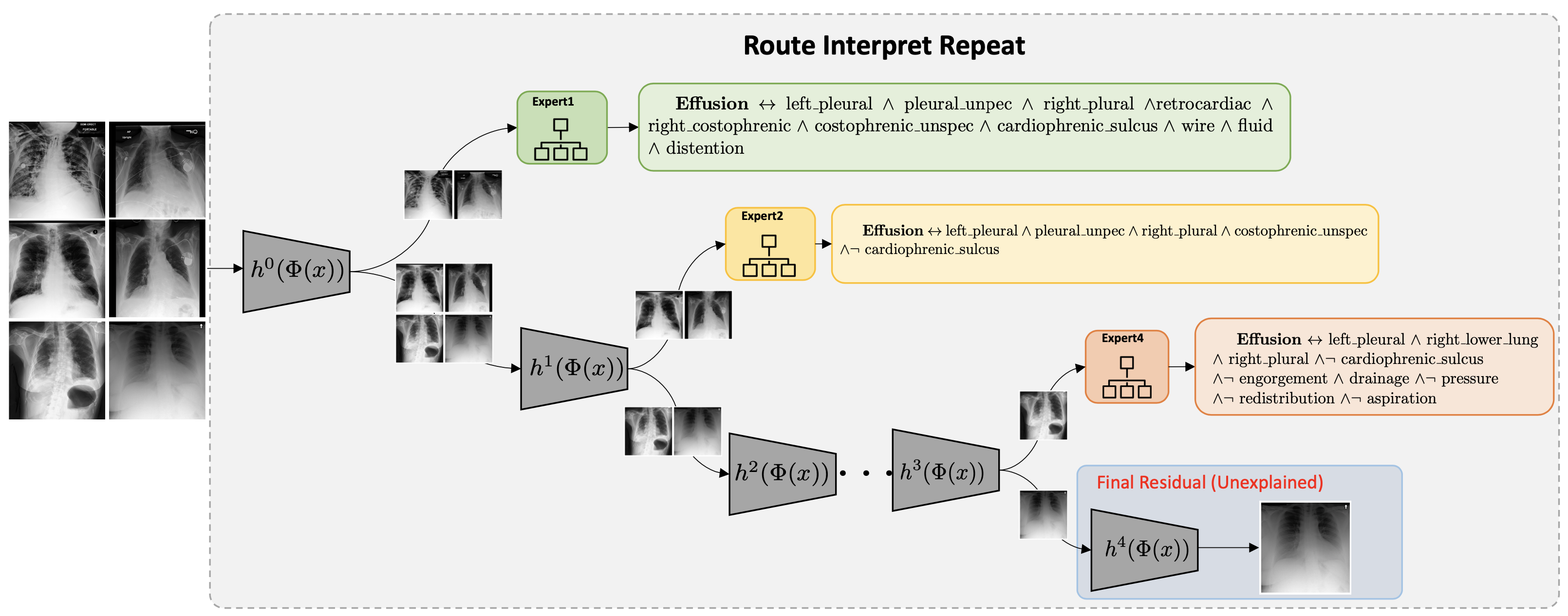
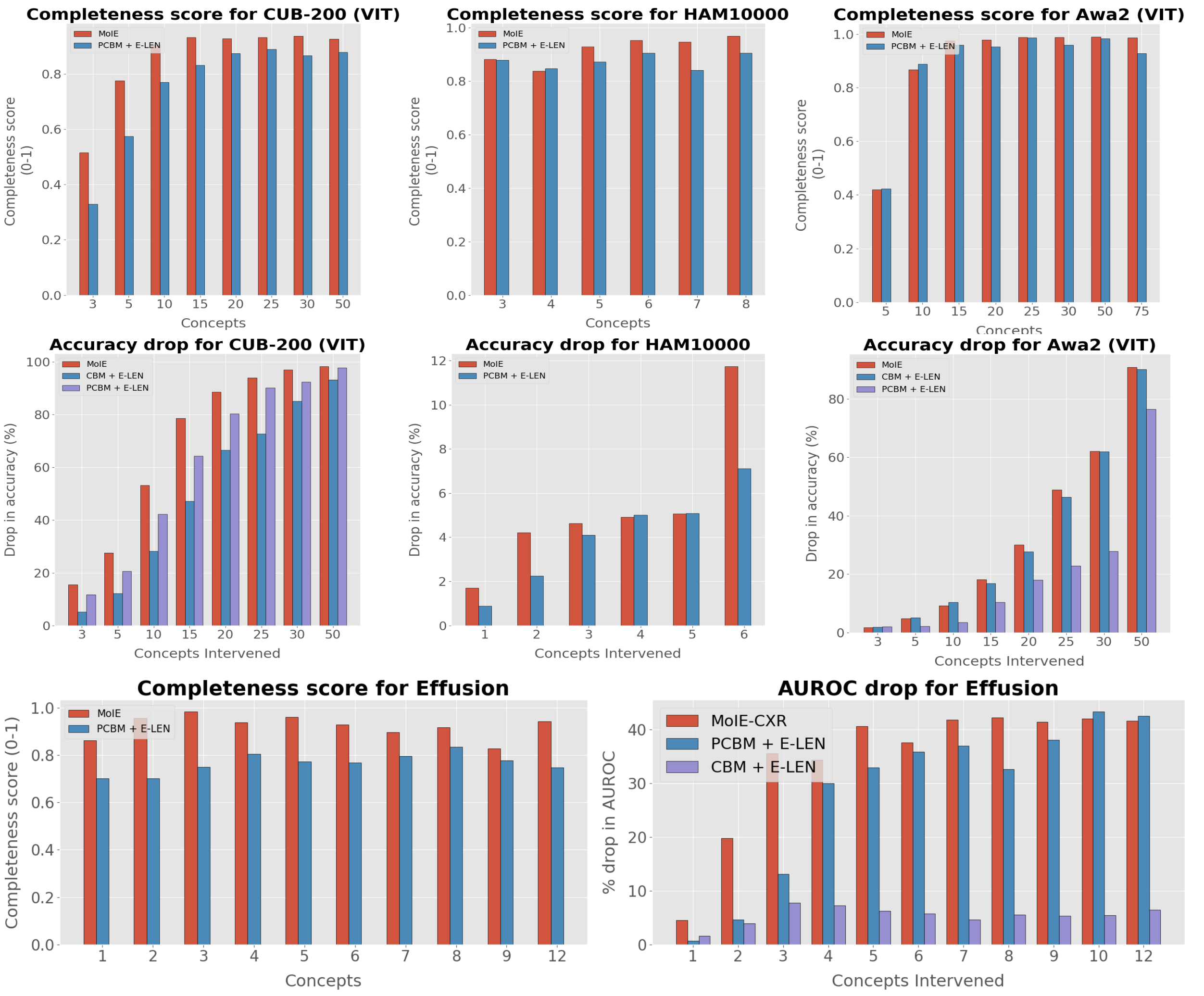
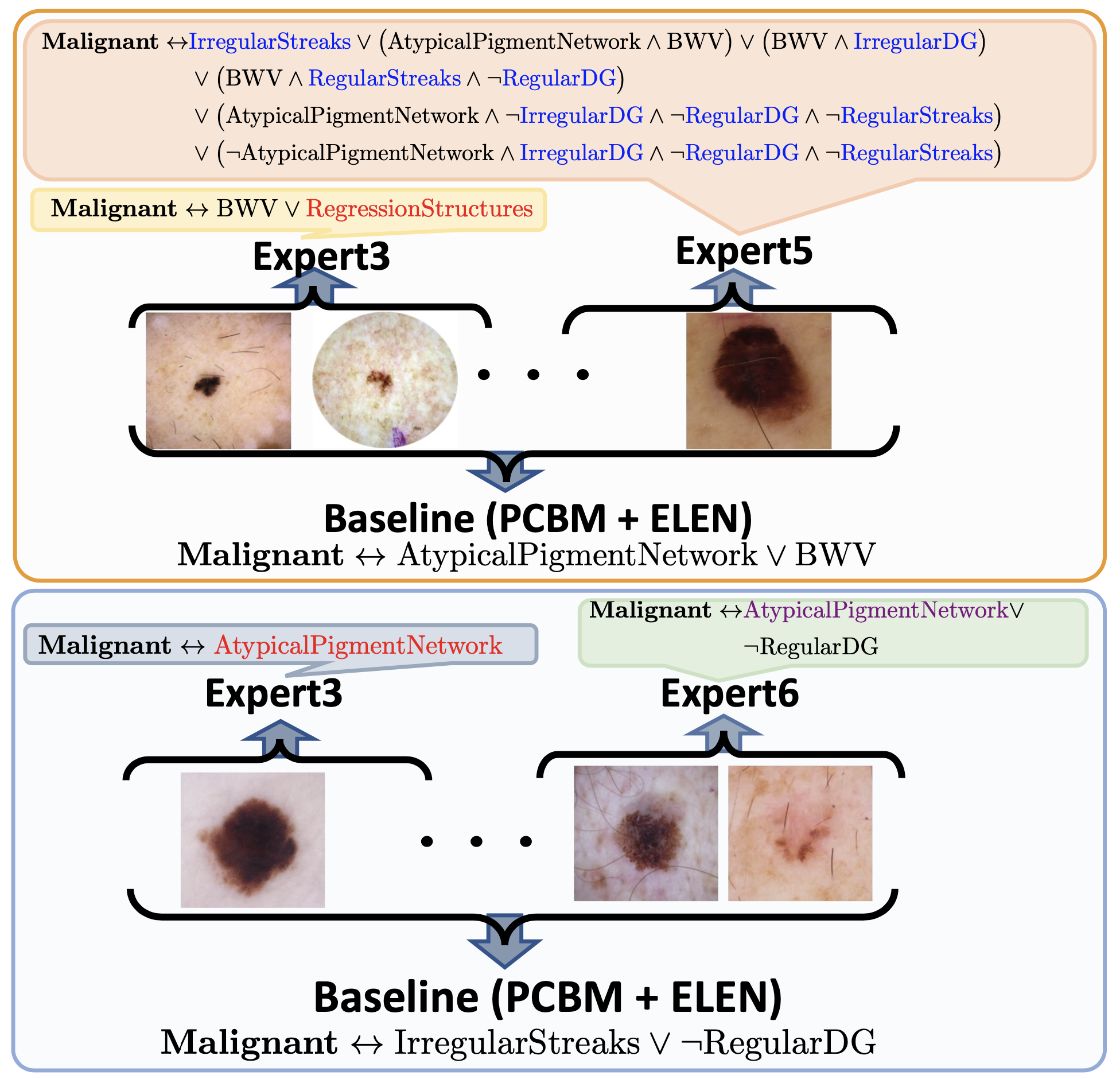
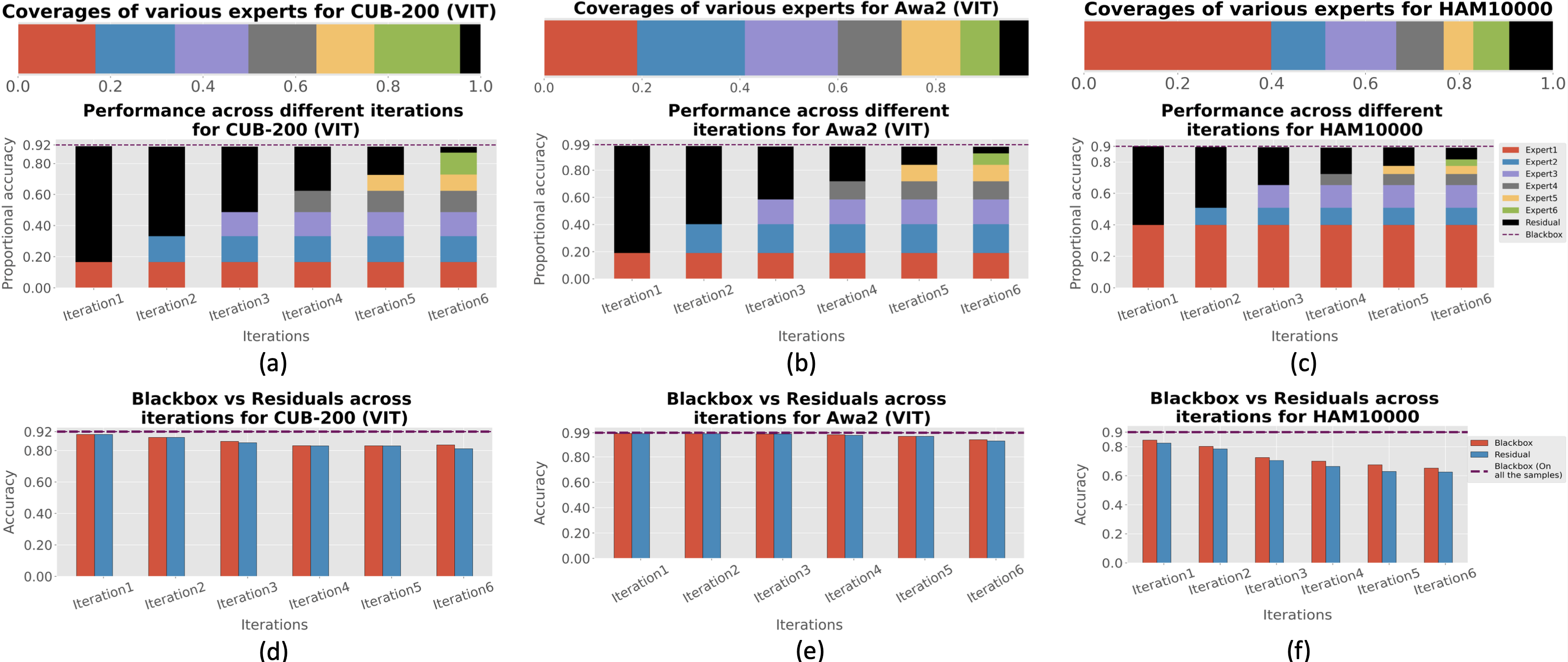
Our contribution. We propose an interpretable method, aiming to achieve the best of both worlds: not sacrificing Blackbox performance similar to post hoc explainability while still providing actionable interpretation. We hypothesize that a Blackbox encodes several interpretable models, each applicable to a different portion of data. We construct a hybrid neuro-symbolic model by progressively carving out a mixture of interpretable models and a residual network from the given Blackbox. We coin the term expert for each interpretable model, as they specialize over a subset of data. All the interpretable models are termed a Mixture of Interpretable Experts (MoIE). Our design identifies a subset of samples and routes them through the interpretable models to explain the samples with First order logic(FOL), providing basic reasoning on concepts from the Blackbox. The remaining samples are routed through a flexible residual network. On the residual network, we repeat the method until MoIE explains the desired proportion of data. Using FOL for interpretable models offers recourse when undesirable behavior is detected in the model. Our method is the divide-and-conquer approach, where the instances covered by the residual network need progressively more complicated interpretable models. 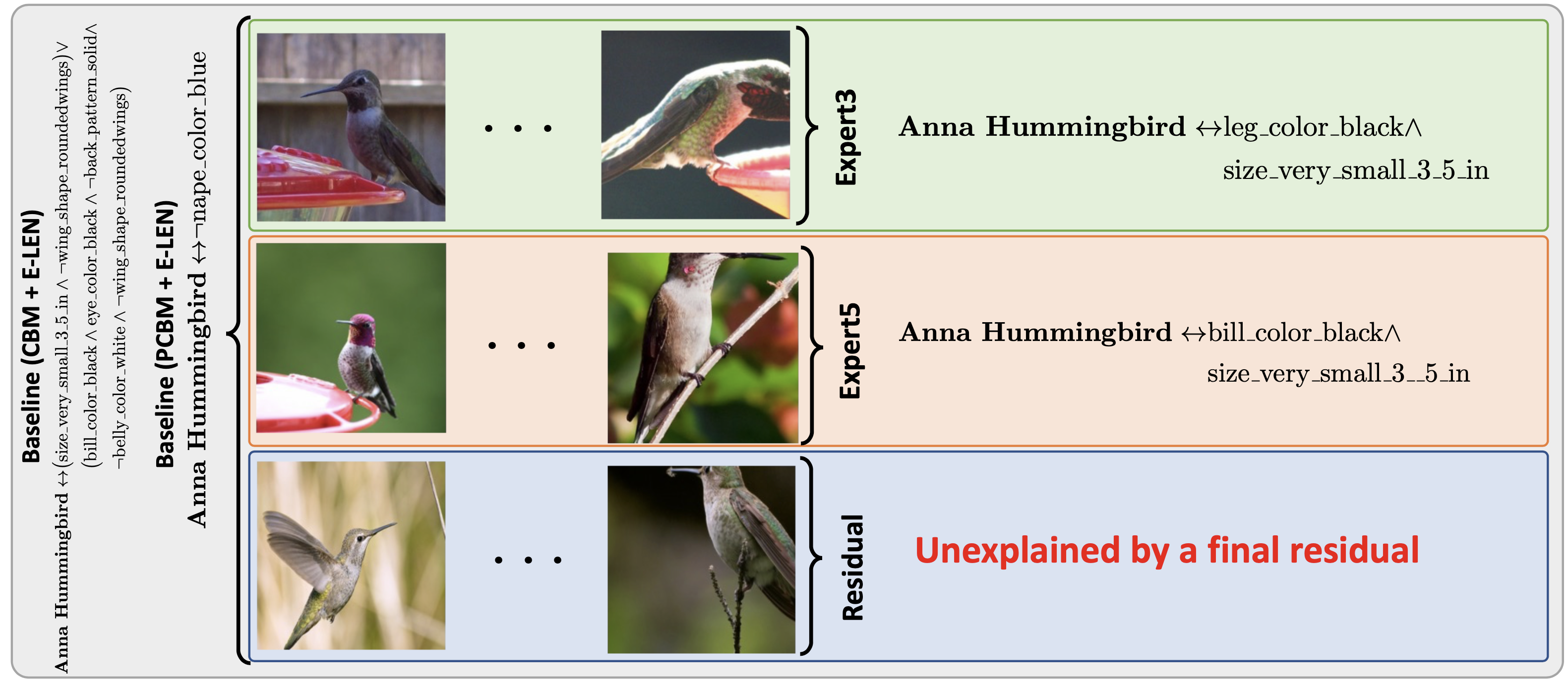Such insight can be used to inspect the data and the model further. Finally, our model allows unexplainable category of data, which is currently not allowed in the interpretable models.

What is a FOL? FOL is a logical function that accepts predicates (concept presence/absent) as input and returns a True/False output being a logical expression of the predicates. The logical expression, which is a set of AND, OR, Negative, and parenthesis, can be written in the so-called Disjunctive Normal Form (DNF). DNF is a FOL logical formula composed of a disjunction (OR) of conjunctions (AND), known as the sum of products.

Assume we have a dataset {X , Y, C}, where X , Y, and C are the input images, class labels, and human interpretable attributes, respectively. Assume f⁰=h⁰(Φ(.)) is the trained Blackbox, where Φ is the representation and h is the classifier. We denote the learnable function t, projecting the image embeddings to the concept space. The concept space is the space spanned by the attributes C. Thus, function t outputs a scalar value representing a concept for each input image.

We iteratively carve out an interpretable model from the given Blackbox. Each iteration yields an interpretable model (the downward grey paths in the above Figure) and a residual (the straightforward black paths in the above Figure 1). We start with the initial Blackbox f⁰. At iteration k, we distill the Blackbox from the previous iteration f^k−1 into a neurosymbolic interpretable model, g^k, predicting the class labels Y from the concepts C. The residual r^k = f^k-1 − g^k emphasizes the portion of f^k-1 that g^k cannot explain. We then approximate r^k with f^k = h^k(Φ(.)). f^k will be the Blackbox for the subsequent iteration and be explained by the respective interpretable model. A learnable gating mechanism, denoted by Π^k: C → {0, 1} (shown as the selector in Figure 1) routes an input sample towards either g^k or r^k. Each interpretable model is learned to focus a specific subset of the data, defined by coverage. The thickness of the lines in Figure represents the samples covered by the interpretable models (grey line) and the residuals (black line). With every iteration, the cumulative coverage of the interpretable models increases, but the residual decreases. We name our method route, interpret and repeat.

We refer to the interpretable models of all the iterations as a Mixture of Interpretable Experts (MoIE) cumulatively after training. Furthermore, we utilize E-LEN, i.e., a Logic Explainable Network implemented with an Entropy Layer as first layer as the interpretable symbolic model g to construct First Order Logic (FOL) explanations of a given prediction.

We perform experiments on a variety of vision and medical imaging datasets to show that 1) MoIE captures a diverse set of concepts, 2) the performance of the residuals degrades over successive iterations as they cover harder instances, 3) MoIE does not compromise the performance of the Blackbox, 4) MoIE achieves superior performances during test time interventions, and 5) MoIE can fix the shortcuts using the Waterbirds dataset. We evaluate our methods using CUB200, Awa2, HAM10000, SIIM-ISIC (real-world transfer learning setting) and MIMIC-CXR (effusion classification) datasets.

Baselines. We compare our methods to two concept-based baselines – 1) interpretable-by-design and 2) posthoc. The end-to-end CEMs and sequential CBMs serve as interpretable-by-design baselines. Similarly, PCBM and PCBM-h serve as post hoc baselines. The standard CBM and PCBM models do not show how the concepts are composed to make the label prediction. So, we create CBM + E-LEN, PCBM + E-LEN and PCBM-h + E-LEN by using the identical g of MOIE, as a replacement for the standard classifiers of CBM and PCBM.